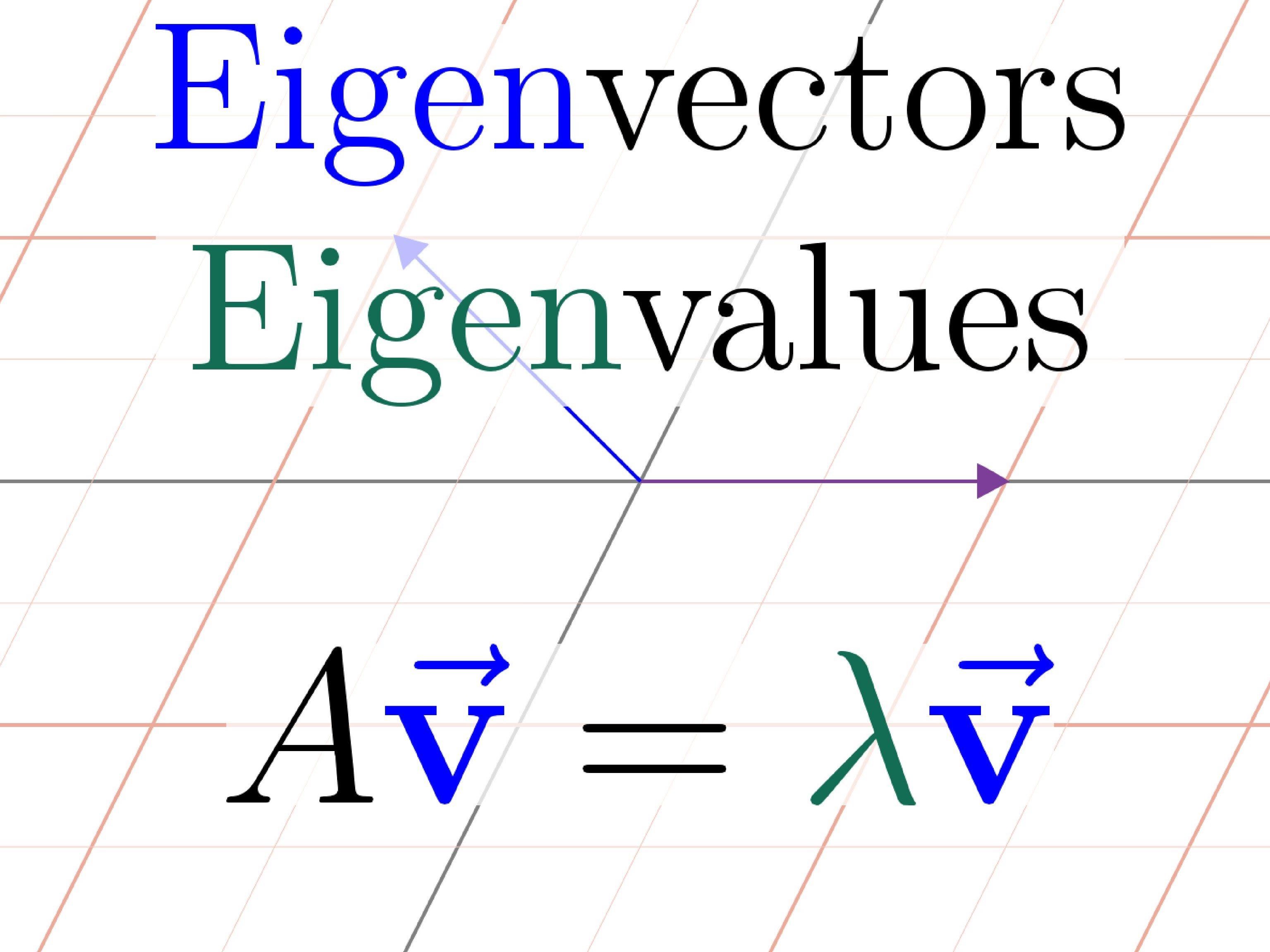About me
Hi, there 👋.
I'm Zixing Wang from China, a Data Analyst working at Bank of Ningbo (Financial Technology Department). Broadly, I am interested in statistical analysis, modeling, prediction, and machine learning.
What i'm doing
-
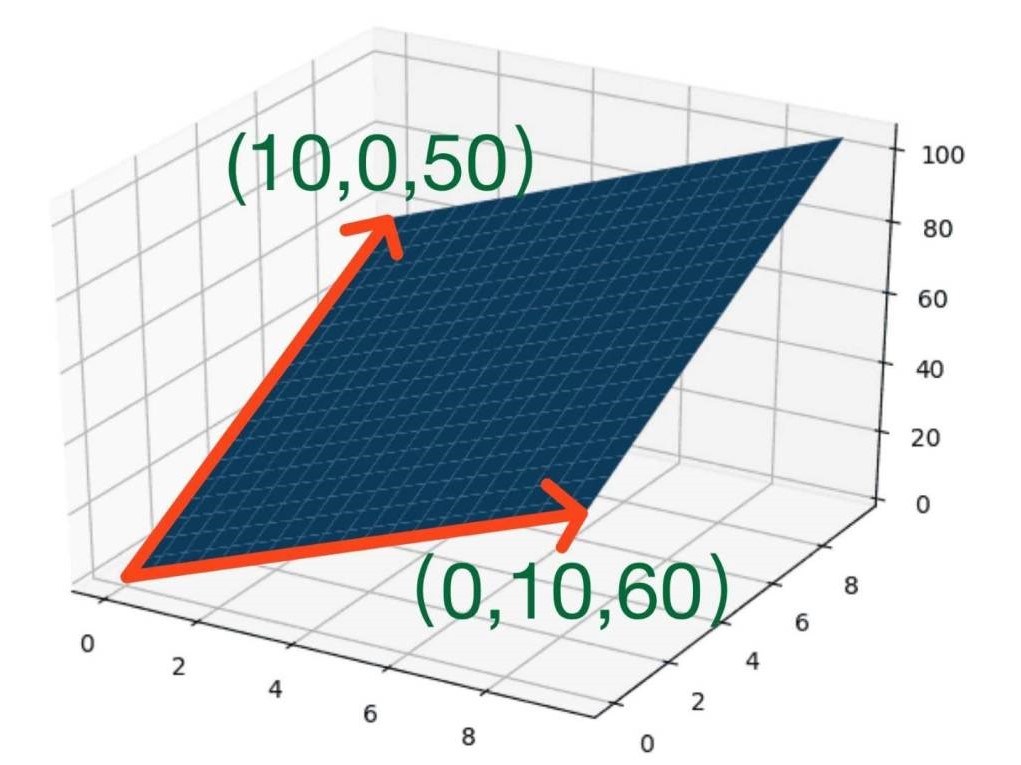
math
I always believe that real math is real fun.
-
read
I like reading books, especially detective fictions.
-
Rubik's cube
I play Rubik's cube and other puzzles.
-
Web development
I design and develop high-quality websites.
Research statement
My interest in statistics grew as my studies progressed, and I found that it was an intriguing area. It is possible to examine the data we collect utilizing the power of statistics. I am excited about statistics by a fascination with randomness, and it brings me to interact with researchers in many areas.
Future direction
I want to engage in statistical analysis, modeling and prediction, to learn and to discover with curiosity.